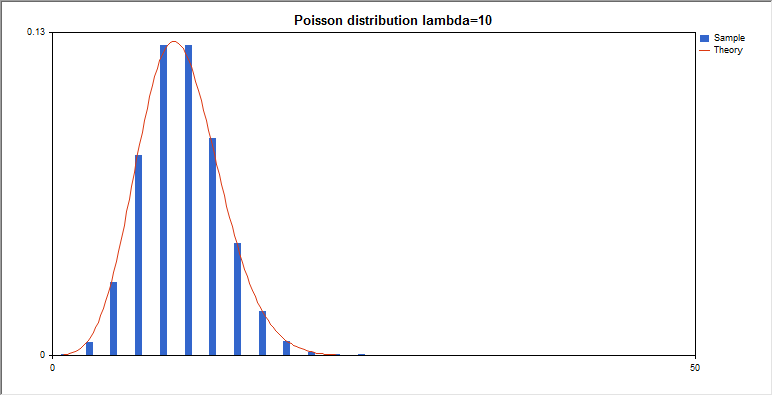
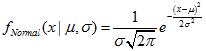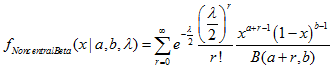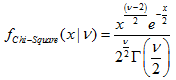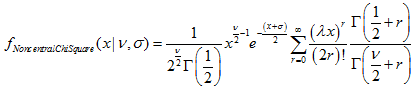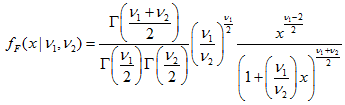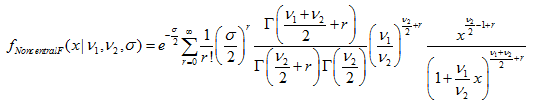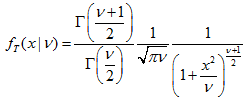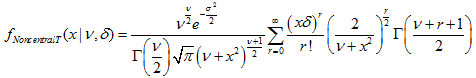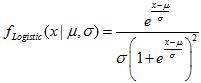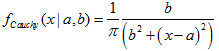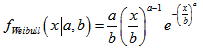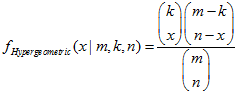統計的特性
この関数グループは、配列要素の統計的特性を計算します。
- 平均、
- 差異、
- 歪み、
- 尖度、
- 中央値、
- 二乗平均平方根、
- 標準偏差
関数 | 説明 |
MathMean | 配列要素の平均 (1次モーメント) を計算します |
MathVariance | 配列要素の差異 (2次モーメント) を計算します |
MathSkewness | 配列要素の歪み (3次モーメント) を計算します |
MathKurtosis | 配列要素の尖度 (4次モーメント) を計算します |
MathMoments | 配列要素の最初の4次のモーメント (平均、分散、歪み度、尖度) を計算します |
MathMedian | 配列要素の中央値を計算します |
MathStandardDeviation | 配列要素の標準偏差を計算します |
MathAverageDeviation | 配列要素の平均絶対偏差を計算します |
正規分布
このセクションには、正規分布を使用するための関数が含まれています。密度、確率、分位数を計算し、正規法則に従って分布した疑似乱数を生成することができます。正規分布は下記の式で定義されています。

ここで
- x — 確率変数の値
- μ — 期待値
- σ — 二乗平均平方根偏差

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityNormal | 正規分布の確率密度関数を計算します |
MathCumulativeDistributionNormal | 正規分布関数の値を計算します |
MathQuantileNormal | 指定された確率に対する正規逆分布関数の値を計算します |
MathRandomNormal | 正規分布の法則に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsNormal | 正規分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatNormal.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double mean_value=0; // 期待値(平均)
input double std_dev=1; // 二乗平均平方根偏差(標準偏差)
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 正規分布からサンプルを取得する
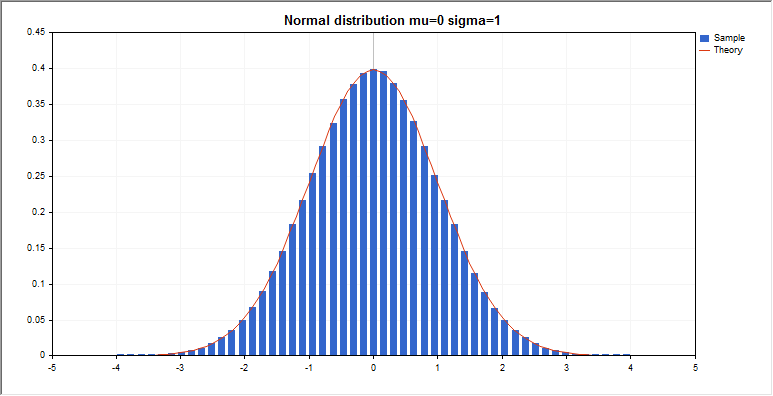
MathRandomNormal(mean_value,std_dev,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityNormal(x2,mean_value,std_dev,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Normal distribution mu=%G sigma=%G”,mean_value,std_dev));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
//— カーブをプロットする
graphic.CurvePlotAll();
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
対数正規分布
このセクションには、対数正規分布を使用するための関数が含まれています。密度、確率、分位数を計算し、対数正規法則に従って分布した疑似乱数を生成することができます。対数正規分布は下記の式で定義されています。

ここで
- x — 確率変数の値
- μ — 期待値の対数
- σ — 二乗平均平方根偏差の対数

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityLognormal | 対数正規分布の確率密度関数を計算します |
MathCumulativeDistributionLognormal | 対数正規分布関数の値を計算します |
MathQuantileLognormal | 指定された確率に対する対数正規逆分布関数の値を計算します |
MathRandomLognormal | 対数正規分布の法則に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsLognormal | 対数正規分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatLognormal.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double mean_value=1.0; // 期待値の対数(対数平均)
input double std_dev=0.25; // 二乗平均平方根偏差の対数(対数標準偏差)
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 対数正規分布からサンプルを取得する
MathRandomLognormal(mean_value,std_dev,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityLognormal(x2,mean_value,std_dev,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Lognormal distribution mu=%G sigma=%G”,mean_value,std_dev));
graphic.BackgroundMainSize(16);
//— Y軸の自動スケーリングを無効にする
graphic.YAxis().AutoScale(false);
graphic.YAxis().Max(theor_max);
graphic.YAxis().Min(0);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
ベータ分布
このセクションには、ベータ分布を使用するための関数が含まれています。密度、確率、分位数を計算し、対応する法則に従って分布した疑似乱数を生成することができます。ベータ分布は下記の式で定義されています。

ここで
- а — ベータ分布の1番目のパラメータ
- b — ベータ分布の2番目のパラメータ

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityBeta | ベータ分布の確率密度関数を計算します |
MathCumulativeDistributionBeta | ベータ確率分布関数の値を計算します |
MathQuantileBeta | 指定された確率に対するベータ逆分布関数の値を計算します |
MathRandomBeta | ベータ分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsBeta | ベータ分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatBeta.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double alpha=2; // ベータ分布の1番目のパラメータ(形状1)
input double beta=5; // ベータ分布の2番目のパラメータ (形状2)
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— ベータ分布からサンプルを取得す
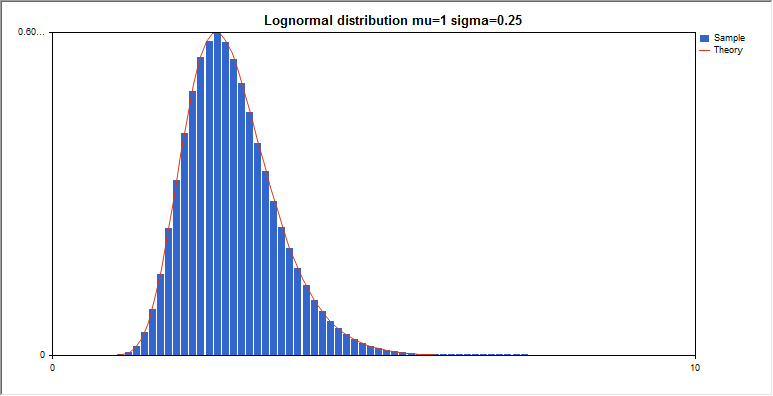
MathRandomBeta(alpha,beta,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityBeta(x2,alpha,beta,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Beta distribution alpha=%G beta=%G”,alpha,beta));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
非心ベータ分布
このセクションには、非心ベータ分布を使用するための関数が含まれています。密度、確率、分位数を計算し、対応する法則に従って分布した疑似乱数を生成することができます。非心ベータ分布は下記の式で定義されています。

ここで
- а — ベータ分布の1番目のパラメータ
- b — ベータ分布の2番目のパラメータ
- λ — 非心パラメータ

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityNoncentralBeta | 非心ベータ分布の確率密度関数を計算します |
MathCumulativeDistributionNoncentralBeta | 非心ベータ確率分布関数の値を計算します |
MathQuantileNoncentralBeta | 指定された確率に対する非心ベータ逆分布関数の値を計算します |
MathRandomNoncentralBeta | 非心ベータ分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsNoncentralBeta | 非心ベータ分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatNoncentralBeta.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double a_par=2; // ベータ分布の1番目のパラメータ(形状1)
input double b_par=5; // ベータ分布の2番目のパラメータ (形状2)
input double l_par=1; // 非心パラメータ (lambda)
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=53; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 非心ベータ分布からサンプルを取得す
MathRandomNoncentralBeta(a_par,b_par,l_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityNoncentralBeta(x2,a_par,b_par,l_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Noncentral Beta distribution alpha=%G beta=%G lambda=%G”,
a_par,b_par,l_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
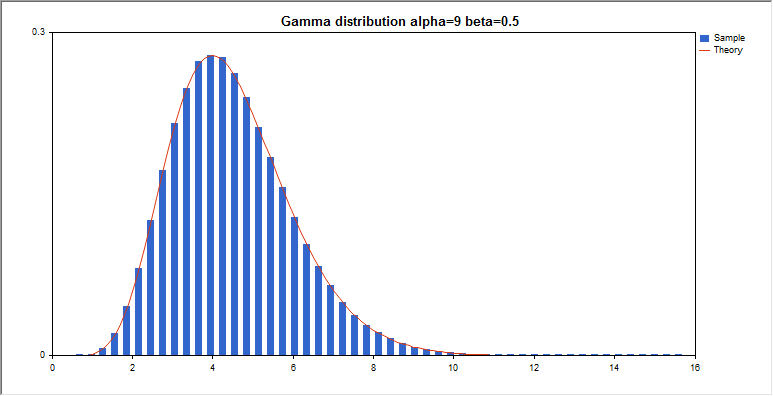
ガンマ分布
このセクションには、ガンマ分布を使用するための関数が含まれています。密度、確率、分位数を計算し、対応する法則に従って分布した疑似乱数を生成することができます。ガンマ分布は下記の式で定義されています。

ここで
- а — 分布の1番目のパラメータ
- b — 分布の2番目のパラメータ

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityGamma | ガンマ分布の確率密度関数を計算します |
MathCumulativeDistributionGamma | ガンマ確率分布関数の値を計算します |
MathQuantileGamma | 指定された確率に対するガンマ逆分布関数の値を計算します |
MathRandomGamma | ガンマ分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsGamma | ガンマ分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatGamma.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double alpha=9; // 分布の1番目のパラメータ(形状)
input double beta=0.5; // 分布の2番目のパラメータ(スケール)
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— ガンマ分布からサンプルを取得する
MathRandomGamma(alpha,beta,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityGamma(x2,alpha,beta,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Gamma distribution alpha=%G beta=%G”,alpha,beta));
graphic.BackgroundMainSize(16);
//— Y軸の自動スケーリングを無効にする
graphic.YAxis().AutoScale(false);
graphic.YAxis().Max(NormalizeDouble(theor_max,1));
graphic.YAxis().Min(0);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
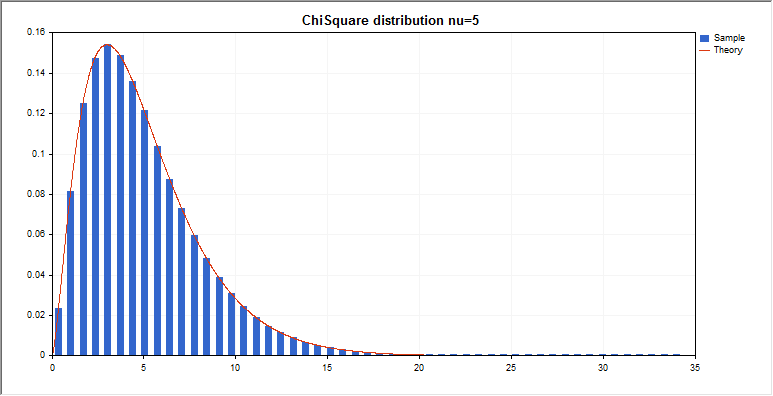
カイ2乗分布
このセクションには、カイ2乗分布を使用するための関数が含まれています。密度、確率、分位数を計算し、対応する法則に従って分布した疑似乱数を生成することができます。カイ2乗分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityChiSquare | カイ2乗分布の確率密度関数を計算します |
MathCumulativeDistributionChiSquare | カイ2乗確率分布関数の値を計算します |
MathQuantileChiSquare | 指定された確率に対するカイ2乗逆分布関数の値を計算します |
MathRandomChiSquare | カイ2乗分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsChiSquare | カイ2乗分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatChiSquare.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double nu_par=5; // 自由度の数
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— カイ2乗分布からサンプルを取得する
MathRandomChiSquare(nu_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityChiSquare(x2,nu_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“ChiSquare distribution nu=%G “,nu_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
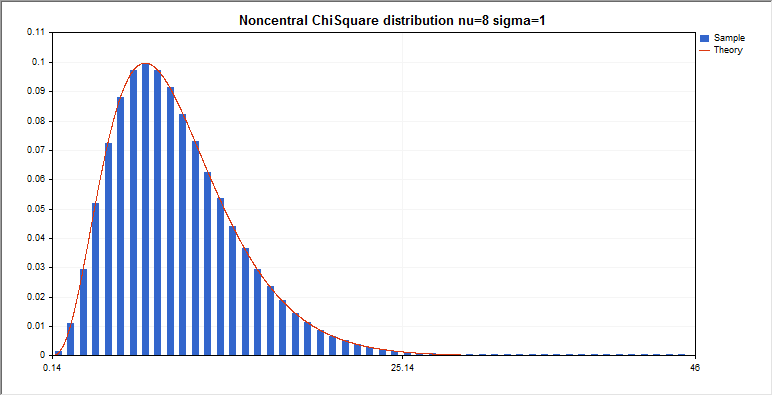
非心カイ2乗分布
このセクションには、非心カイ2乗分布を使用するための関数が含まれています。密度、確率、分位数を計算し、対応する法則に従って分布した疑似乱数を生成することができます。非心カイ2乗分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityNoncentralChiSquare | 非心カイ2乗分布の確率密度関数を計算します |
MathCumulativeDistributionNoncentralChiSquare | 非心カイ2乗確率分布関数の値を計算します |
MathQuantileNoncentralChiSquare | 指定された確率に対する非心カイ2乗逆分布関数の値を計算します |
MathRandomNoncentralChiSquare | 非心カイ2乗分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsNoncentralChiSquare | 非心カイ2乗分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatNoncentralChiSquare.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double nu_par=8; // 自由度の数
input double si_par=1; // 非心パラメータ
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 非新カイ2乗分布からサンプルを取得する
MathRandomNoncentralChiSquare(nu_par,si_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityNoncentralChiSquare(x2,nu_par,si_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Noncentral ChiSquare distribution nu=%G sigma=%G”,nu_par,si_par));
graphic.BackgroundMainSize(16);
//— Y軸の自動スケーリングを無効にする
graphic.XAxis().AutoScale(false);
graphic.XAxis().Max(NormalizeDouble(max,0));
graphic.XAxis().Min(min);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
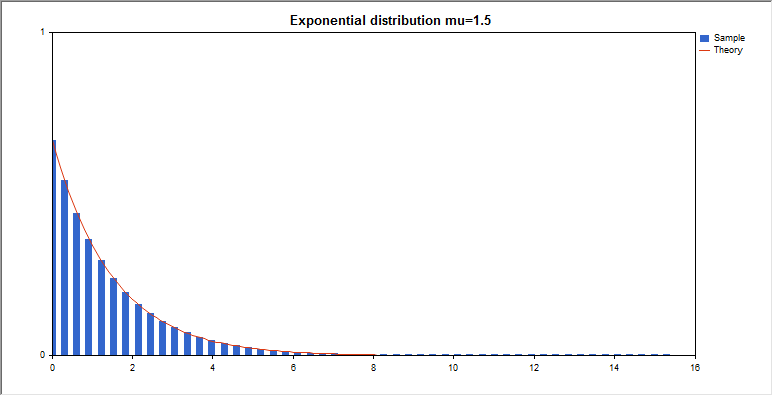
指数
このセクションには、指数分布を使用するための関数が含まれています。密度、確率、分位数を計算し、指数分布に従って分布した疑似乱数を生成することができます。指数分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityExponential | 指数分布の確率密度関数を計算します |
MathCumulativeDistributionExponential | 指数確率分布関数の値を計算します |
MathQuantileExponential | 指定された確率に対する指数逆分布関数の値を計算します |
MathRandomExponential | 指数分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsExponential | 指数分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatExponential.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double mu_par=1.5; // 自由度の数
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 指数分布からサンプルを取得する
MathRandomExponential(mu_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityExponential(x2,mu_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Exponential distribution mu=%G “,mu_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+i*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
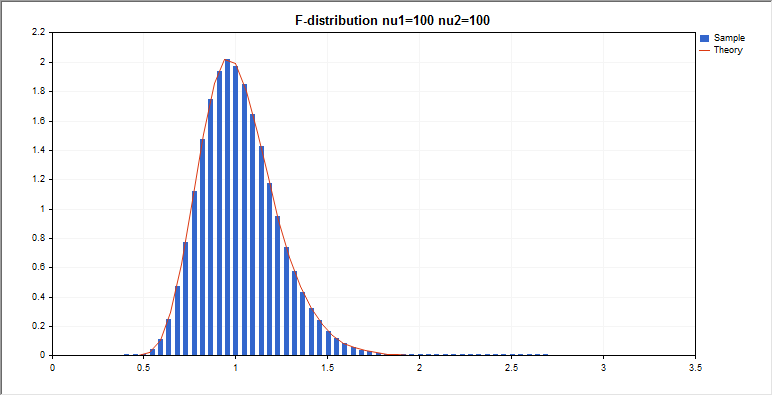
F分布
このセクションには、F分布を使用するための関数が含まれています。密度、確率、分位数を計算し、F分布に従って分布した疑似乱数を生成することができます。F分布は下記の式で定義されています。

ここで
- ν1 — 分布の1番目のパラメータ(自由度の数)
- ν2 — 分布の2番目のパラメータ(自由度の数)</

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityF | F分布の確率密度関数を計算します |
MathCumulativeDistributionF | F分布関数の値を計算します |
MathQuantileF | 指定された確率に対するF逆分布関数の値を計算します |
MathRandomF | F分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsF | F分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatF.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double nu_1=100; // 1番目の自由度の数
input double nu_2=100; // 2番目の自由度の数
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— フィッシャーのF分布からサンプルを取得する
MathRandomF(nu_1,nu_2,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityF(x2,nu_1,nu_2,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“F-distribution nu1=%G nu2=%G”,nu_1,nu_2));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(4);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
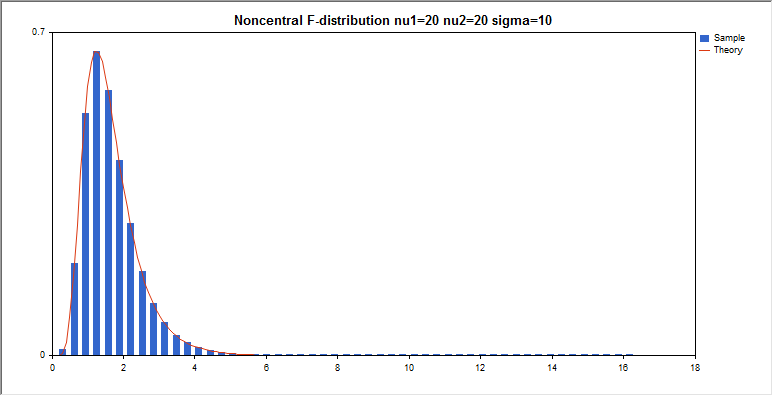
非心F分布
このセクションには、非心F分布を使用するための関数が含まれています。密度、確率、分位数を計算し、非心F分布に従って分布した疑似乱数を生成することができます。非心F分布は下記の式で定義されています。

ここで
- ν1 — 分布の1番目のパラメータ(自由度の数)
- ν2 — 分布の2番目のパラメータ(自由度の数)</

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityNoncentralF | 非心F分布の確率密度関数を計算します |
MathCumulativeDistributionNoncentralF | 非心F分布関数の値を計算します |
MathQuantileNoncentralF | 指定された確率に対する非心F逆分布関数の値を計算します |
MathRandomNoncentralF | 非心F分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsNoncentralF | 非心F分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatNoncentralF.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double nu_1=20; // 1番目の自由度の数
input double nu_2=20; // 2番目の自由度の数
input double sig=10; // 非心パラメータ
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— フィッシャーのF分布からサンプルを取得する
MathRandomNoncentralF(nu_1,nu_2,sig,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityNoncentralF(x2,nu_1,nu_2,sig,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Noncentral F-distribution nu1=%G nu2=%G sigma=%G”,nu_1,nu_2,sig));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
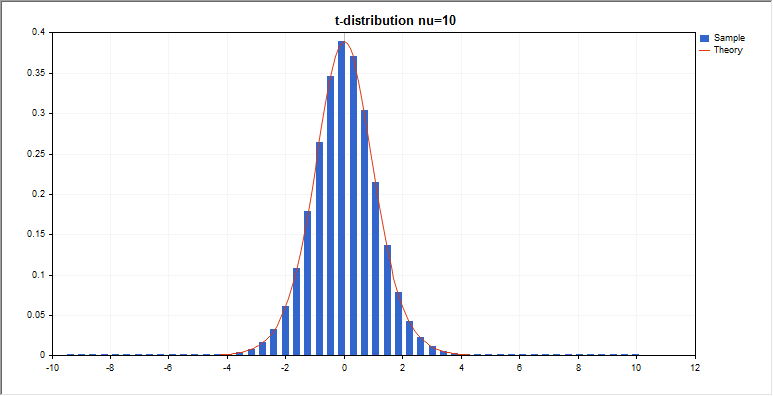
t分布
このセクションには、スチューデントのt分布を使用するための関数が含まれています。密度、確率、分位数を計算し、スチューデントのt分布法則に従って分布した疑似乱数を生成することができます。スチューデントのt分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityT | スチューデントのt分布の確率密度関数を計算します |
MathCumulativeDistributionT | t分布関数の値を計算します |
MathQuantileT | 指定された確率に対するt逆分布関数の値を計算します |
MathRandomT | t分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsT | スチューデントのt分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatT.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double nu_par=10; // 自由度の数
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— スチューデントのt分布からサンプルを取得する
MathRandomT(nu_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityT(x2,nu_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“t-distribution nu=%G”,nu_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
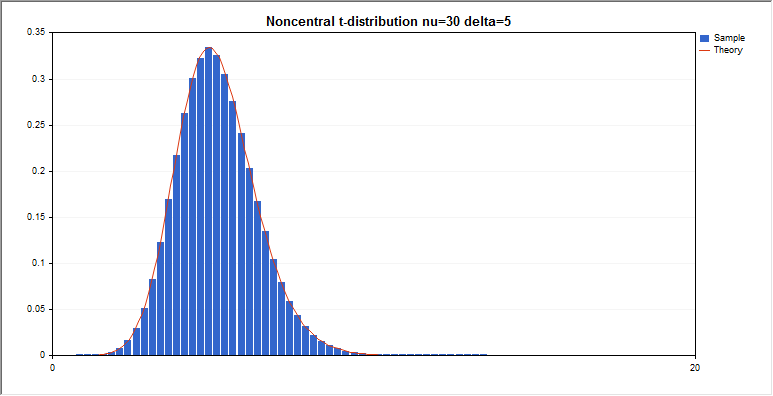
t分布
このセクションには、非心t分布を使用するための関数が含まれています。密度、確率、分位数を計算し、非心t分布に従って分布した疑似乱数を生成することができます。非心t分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityNoncentralT | 非心t分布の確率密度関数を計算します |
MathCumulativeDistributionNoncentralT | 非心t分布関数の値を計算します |
MathQuantileNoncentralT | 指定された確率に対する非心t逆分布関数の値を計算します |
MathRandomNoncentralT | 非心t分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsNoncentralT | 非心t分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatNoncentralT.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double nu_par=30; // 自由度の数
input double delta_par=5; // 非心パラメータ
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 非心t分布からサンプルを取得する
MathRandomNoncentralT(nu_par,delta_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityNoncentralT(x2,nu_par,delta_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Noncentral t-distribution nu=%G delta=%G”,nu_par,delta_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
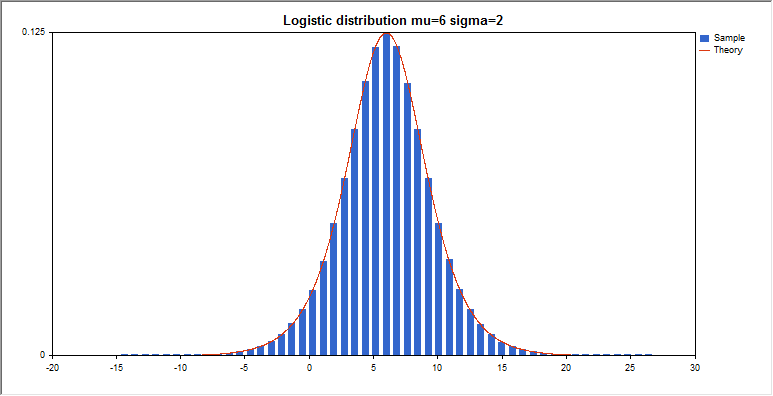
ロジスティック分布
このセクションには、ロジスティック分布を使用するための関数が含まれています。密度、確率、分位数を計算し、ロジスティック法則に従って分布した疑似乱数を生成することができます。ロジスティック分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityLogistic | ロジスティック分布の確率密度関数を計算します |
MathCumulativeDistributionLogistic | ロジスティック確率分布関数の値を計算します |
MathQuantileLogistic | 指定された確率に対するロジスティック逆分布関数の値を計算します |
MathRandomLogistic | ロジスティック分布の法則に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsLogistic | ロジスティック分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatLogistic.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double mu_par=6; // 分布の平均パラメータ
input double sigma_par=2; // 分布のスケールパラメータ
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— ロジスティク分布からサンプルを取得する
MathRandomLogistic(mu_par,sigma_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityLogistic(x2,mu_par,sigma_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Logistic distribution mu=%G sigma=%G”,mu_par,sigma_par));
graphic.BackgroundMainSize(16);
//— Y軸の自動スケーリングを無効にする
graphic.YAxis().AutoScale(false);
graphic.YAxis().Max(theor_max);
graphic.YAxis().Min(0);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
コーシー分布
このセクションには、コーシー分布を使用するための関数が含まれています。密度、確率、分位数を計算し、コーシー法則に従って分布した疑似乱数を生成することができます。コーシー分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityCauchy | コーシー分布の確率密度関数を計算します |
MathCumulativeDistributionCauchy | コーシー確率分布関数の値を計算します |
MathQuantileCauchy | 指定された確率に対するコーシー逆分布関数の値を計算します |
MathRandomCauchy | コーシー分布の法則に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsCauchy | コーシー分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatCauchy.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double a_par=-2; // 分布の平均パラメータ
input double b_par=1; // 分布のスケールパラメータ
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— コーシー分布からサンプルを取得する
MathRandomCauchy(a_par,b_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityCauchy(x2,a_par,b_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
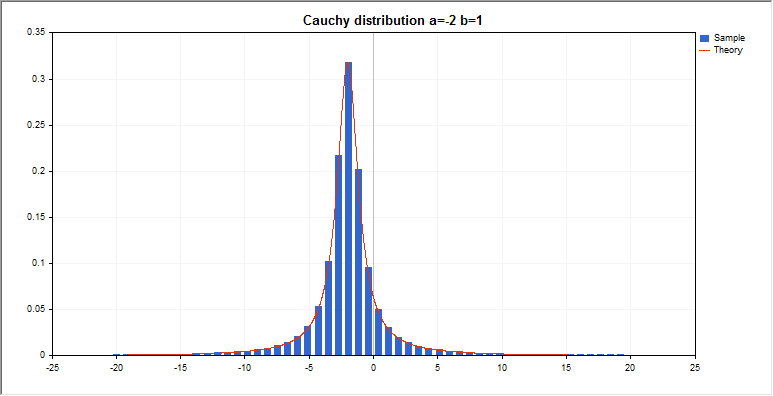
graphic.BackgroundMain(StringFormat(“Cauchy distribution a=%G b=%G”,a_par,b_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1)
return(false);
int size=ArraySize(data);
if(size<cells*10)
return(false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
Print(“min=”,minv,” max=”,maxv);
minv=-20;
maxv=20;
double range=maxv-minv;
double width=range/cells;
if(width==0)
return(false);
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+i*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=(int)MathRound((data[i]-minv)/width);
if(ind>=0 && ind<cells)
frequency[ind]++;
}
return(true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
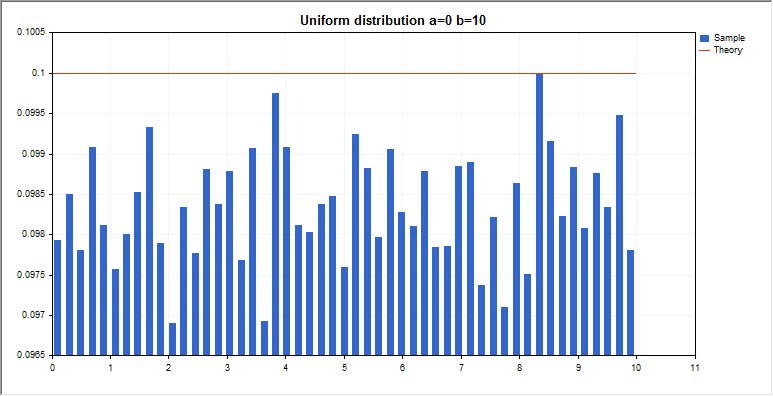
一様分布
このセクションには、一様分布を使用するための関数が含まれています。密度、確率、分位数を計算し、一様分布の法則に従って分布した疑似乱数を生成することができます。一様分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityUniform | 一様分布の確率密度関数を計算します |
MathCumulativeDistributionUniform | 一様確率分布関数の値を計算します |
MathQuantileUniform | 指定された確率に対する一様逆分布関数の値を計算します |
MathRandomUniform | 一様分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsUniform | 一様分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatUniform.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double a_par=0; // 分布のパラメータa(下限)
input double b_par=10; // 分布のパラメータb(上限)
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 一様分布からサンプルを取得する
MathRandomUniform(a_par,b_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityUniform(x2,a_par,b_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Uniform distribution a=%G b=%G”,a_par,b_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
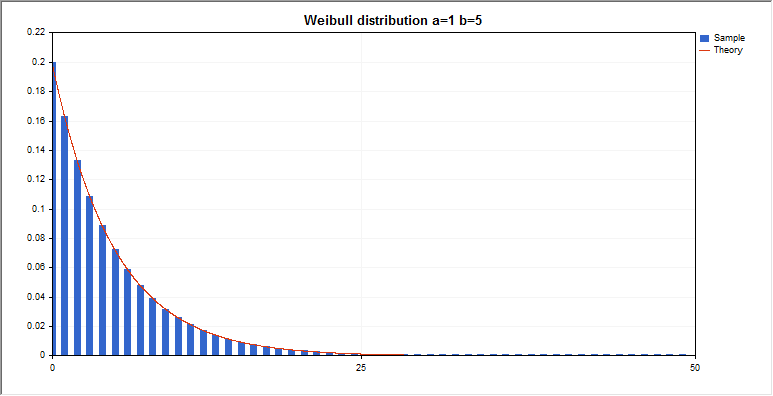
ワイブル分布
このセクションには、ワイブル分布を使用するための関数が含まれています。密度、確率、分位数を計算し、ワイブル分布の法則に従って分布した疑似乱数を生成することができます。ワイブル分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityWeibull | ワイブル分布の確率密度関数を計算します |
MathCumulativeDistributionWeibull | ワイブル確率分布関数の値を計算します |
MathQuantileWeibull | 指定された確率に対するワイブル逆分布関数の値を計算します |
MathRandomWeibull | ワイブル分布の法則に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsWeibull | ワイブル分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatWeibull.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double a_par=1; // 分布のパラメータ(形状)
input double b_par=5; // 分布のパラメータ(スケール)
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=51; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— ワイブル分布からサンプルを取得する
MathRandomWeibull(a_par,b_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityWeibull(x2,a_par,b_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Weibull distribution a=%G b=%G”,a_par,b_par));
graphic.BackgroundMainSize(16);
//— Y軸の自動スケーリングを無効にする
graphic.XAxis().AutoScale(false);
graphic.XAxis().Max(max);
graphic.XAxis().Min(min);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+i*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
二項分布
このセクションには、二項分布を使用するための関数が含まれています。密度、確率、分位数を計算し、二項法則に従って分布した疑似乱数を生成することができます。二項分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityBinomial | 二項分布の確率密度関数を計算します |
MathCumulativeDistributionBinomial | 二項確率分布関数の値を計算します |
MathQuantileBinomial | 指定された確率に対する二項逆分布関数の値を計算します |
MathRandomBinomial | 二項分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsBinomial | 二項分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatBinomial.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double n_par=40; // テスト数
input double p_par=0.75; // 各テストの成功率
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=20; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 二項分布からサンプルを取得する
MathRandomBinomial(n_par,p_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(0,n_par,1,x2);
MathProbabilityDensityBinomial(x2,n_par,p_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Binomial distributionn n=%G p=%G”,n_par,p_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”).LinesSmooth(true);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
} |
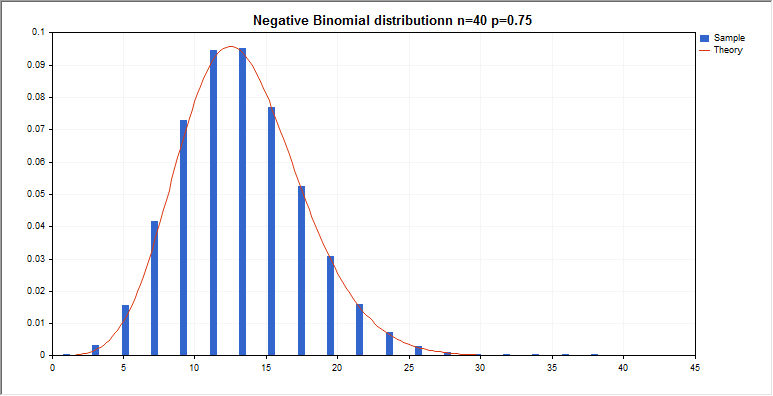
負の二項分布
このセクションには、負の二項分布を使用するための関数が含まれています。密度、確率、分位数を計算し、負の二項法則に従って分布した疑似乱数を生成することができます。負の二項分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityNegativeBinomial | 負の二項分布の確率密度関数を計算します |
MathCumulativeDistributionNegativeBinomial | 負の二項確率分布関数の値を計算します |
MathQuantileNegativeBinomial | 指定された確率に対する負の二項逆分布関数の値を計算します |
MathRandomNegativeBinomial | 負の二項分布に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsNegativeBinomial | 負の二項分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatNegativeBinomial.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double n_par=40; // テスト数
input double p_par=0.75; // 各テストの成功率
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=19; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 負の二項分布からサンプルを取得する
MathRandomNegativeBinomial(n_par,p_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(0,n_par,1,x2);
MathProbabilityDensityNegativeBinomial(x2,n_par,p_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Negative Binomial distributionn n=%G p=%G”,n_par,p_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”).LinesSmooth(true);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
} |
幾何分布
このセクションには、幾何分布を使用するための関数が含まれています。密度、確率、分位数を計算し、幾何法則に従って分布した疑似乱数を生成することができます。幾何分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityGeometric | 幾何分布の確率密度関数を計算します |
MathCumulativeDistributionGeometric | 幾何確率分布関数の値を計算します |
MathQuantileGeometric | 指定された確率に対する幾何逆分布関数の値を計算します |
MathRandomGeometric | 幾何分布の法則に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsGeometric | 幾何分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatGeometric.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double p_par=0.2; // 1回のテストでのイベント発生率
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=47; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 幾何分布からサンプルを取得する
MathRandomGeometric(p_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
PrintFormat(“max=%G min=%G”,max,min);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(0,ncells,1,x2);
MathProbabilityDensityGeometric(x2,p_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Geometric distribution p=%G”,p_par));
graphic.BackgroundMainSize(16);
//— Y軸の自動スケーリングを無効にする
graphic.XAxis().AutoScale(false);
graphic.XAxis().Max(max);
graphic.XAxis().Min(min);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+i*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
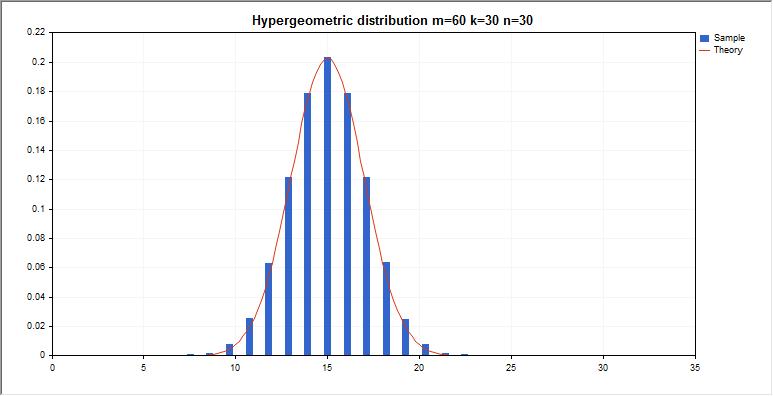
超幾何分布
このセクションには、超幾何分布を使用するための関数が含まれています。密度、確率、分位数を計算し、超幾何法則に従って分布した疑似乱数を生成することができます。超幾何分布は下記の式で定義されています。

ここで
- m — オブジェクトの総数
- k — 所望の特性を有するオブジェクトの数
- n — オブジェクト描画の数

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityHypergeometric | 超幾何分布の確率密度関数を計算します |
MathCumulativeDistributionHypergeometric | 超幾何確率分布関数の値を計算します |
MathQuantileHypergeometric | 指定された確率に対する超幾何逆分布関数の値を計算します |
MathRandomHypergeometric | 超幾何分布の法則に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsHypergeometric | 超幾何分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatHypergeometric.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double m_par=60; // オブジェクトの総数
input double k_par=30; // 所望の特性を有するオブジェクトの数
input double n_par=30; // オブジェクト描画の数
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=1000000; // サンプルの値の数
int ncells=15; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— 超幾何分布からサンプルを取得する
MathRandomHypergeometric(m_par,k_par,n_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
PrintFormat(“max=%G min=%G”,max,min);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(0,n_par,1,x2);
MathProbabilityDensityHypergeometric(x2,m_par,k_par,n_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Hypergeometric distribution m=%G k=%G n=%G”,m_par,k_par,n_par));
graphic.BackgroundMainSize(16);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”).LinesSmooth(true);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
ポアソン分布
このセクションには、ポアソン分布を使用するための関数が含まれています。密度、確率、分位数を計算し、ポアソン法則に従って分布した疑似乱数を生成することができます。ポアソン分布は下記の式で定義されています。

ここで

ライブラリは、個々の確率変数の計算に加えて、確率変数の配列を扱う能力も実装しています。
関数 | 説明 |
MathProbabilityDensityPoisson | ポアソン分布の確率密度関数を計算します |
MathCumulativeDistributionPoisson | ポアソン確率分布関数の値を計算します |
MathQuantilePoisson | 指定された確率に対するポアソン逆分布関数の値を計算します |
MathRandomPoisson | ポアソン分布の法則に従って分布した擬似乱数変数/擬似乱数変数の配列を生成します |
MathMomentsPoisson | ポアソン分布の最初の4次のモーメントの理論的数値を計算します |
例:
#include <GraphicsGraphic.mqh>
#include <MathStatPoisson.mqh>
#include <MathStatMath.mqh>
#property script_show_inputs
//— 入力パラメータ
input double lambda_par=10; // 分布のパラメータ(平均)
//+——————————————————————+
//| スクリプトプログラムを開始する関数 |
//+——————————————————————+
void OnStart()
{
//— 価格チャートを非表示にする
ChartSetInteger(0,CHART_SHOW,false);
//— 擬似乱数生成器を初期化する
MathSrand(GetTickCount());
//— 確率変数のサンプルを生成する
long chart=0;
string name=“GraphicNormal”;
int n=100000; // サンプルの値の数
int ncells=13; // ヒストグラムの間隔の数
double x[]; // ヒストグラム間隔の中心
double y[]; // 間隔内のサンプルからの値の数
double data[]; // 確率変数値のサンプル
double max,min; // サンプルの最大値と最小値
//— ポアソン分布からサンプルを取得する
MathRandomPoisson(lambda_par,n,data);
//— ヒストグラムをプロットするためのデータを計算する
CalculateHistogramArray(data,x,y,max,min,ncells);
//— 理論曲線をプロットするシーケンス境界とステップを取得する
double step;
GetMaxMinStepValues(max,min,step);
PrintFormat(“max=%G min=%G”,max,min);
//— [min、max]の間隔で理論的に計算されたデータを取得する
double x2[];
double y2[];
MathSequence(0,int(MathCeil(max)),1,x2);
MathProbabilityDensityPoisson(x2,lambda_par,false,y2);
//— 規模を設定する
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//— チャートを出力する
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat(“Poisson distribution lambda=%G”,lambda_par));
graphic.BackgroundMainSize(16);
//— Y軸の自動スケーリングを無効にする
graphic.YAxis().AutoScale(false);
graphic.YAxis().Max(NormalizeDouble(theor_max,2));
graphic.YAxis().Min(0);
//— カーブをプロットする
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,“Sample”).HistogramWidth(6);
//— 今度は分布密度の理論曲線をプロットする
graphic.CurveAdd(x2,y2,CURVE_LINES,“Theory”).LinesSmooth(true);
graphic.CurvePlotAll();
//— カーブをプロットする
graphic.Update();
}
//+——————————————————————+
//| データセットの頻度を計算する |
//+——————————————————————+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//— 間隔の中心を定義する
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//— 間隔内に入る頻度を記入する
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+——————————————————————+
//| シーケンス生成の値を計算する |
//+——————————————————————+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//— 正規化の精度を得るためにシーケンスの絶対範囲を計算する
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//— 最大値と最小値を指定された精度に正規化する
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//— 指定された精度に基づいてシーケンス生成ステップも設定される
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
} |
サブ関数
ガンマ関数、ベータ関数、階乗、指数関数、異なる基底を持つ対数、平方根などの基本的な数学演算を実行する関数のグループです。
これらは、個々の数値(実数と整数)と値の配列(別々の配列または元の配列への結果の出力)を処理する機能を備えています。
関数 | 説明 |
MathRandomNonZero | 0.0〜1.0の浮動小数点数を持つ乱数を返します。 |
MathMoments | 配列要素の最初の四次モーメント(平均、分散、歪度、尖度)を計算します。 |
MathPowInt | 数を指定された整数乗まで引き上げます。 |
MathFactorial | 指定された整数の階乗を計算します。 |
MathTrunc | 指定された数値や配列要素の整数部分を計算します。 |
MathRound | 数値または数値の配列を指定された小数点以下桁数に丸めます。 |
MathArctan2 | 接線が[-pi、pi]の範囲にある指定された2つの数値の比率に等しい角度を計算します。 |
MathGamma | ガンマ関数の値を計算します。 |
MathGammaLog | ガンマ関数の対数を計算します。 |
MathBeta | ベータ関数の値を計算します。 |
MathBetaLog | ベータ関数の対数を計算します。 |
MathBetaIncomplete | 不完全ベータ関数の値を計算します。 |
MathGammaIncomplete | 不完全ガンマ関数の値を計算します。 |
MathBinomialCoefficient | 二項係数を計算します。 |
MathBinomialCoefficientLog | 二項係数の対数を計算します。 |
MathHypergeometric2F2 | 超幾何関数の値を計算します。 |
MathSequence | 最初の要素、最後の要素、シーケンスのステップの値に基づいてシーケンスを生成します。 |
MathSequenceByCount | 最初の要素、最後の要素、シーケンスの要素数に基づいてシーケンスを生成します。 |
MathReplicate | 繰り返し値のシーケンスを生成します。 |
MathReverse | 要素を逆順にした値の配列を生成します。 |
MathIdentical | 2つの値の配列を比較し、すべての要素が一致する場合はtrueを返します。 |
MathUnique | 一意の値のみを持つ配列を生成します。 |
MathQuickSortAscending | 昇順で並べ替える関数です。 |
MathQuickSortDescending | 降順で並べ替える関数です。 |
MathQuickSort | 並べ替え関数です。 |
MathOrder | 並べ替え後の配列要素の順番に従った順列を持つ配列を生成します。 |
MathBitwiseNot | 配列要素のビット単位NOT演算の結果を計算します。 |
MathBitwiseAnd | 配列要素のビット単位AND演算の結果を計算します。 |
MathBitwiseOr | 配列要素のビット単位AND演算の結果を計算します。 |
MathBitwiseXor | 配列要素のビット単位XOR演算の結果を計算します。 |
MathBitwiseShiftL | 配列要素のビット単位SHL演算の結果を計算します。 |
MathBitwiseShiftR | 配列要素のビット単位SHR演算の結果を計算します。 |
MathCumulativeSum | 累積合計で配列を生成します。 |
MathCumulativeProduct | 累積積で配列を生成します。 |
MathCumulativeMin | 累積最小値で配列を生成します。 |
MathCumulativeMax | 累積最大値で配列を生成します。 |
MathSin | 配列要素のsin(x)関数の値を計算します。 |
MathCos | 配列要素のcos(x)関数の値を計算します。 |
MathTan | 配列要素のtan(x)関数の値を計算します。 |
MathArcsin | 配列要素のarcsin(x)関数の値を計算します。 |
MathArccos | 配列要素のarccos(x)関数の値を計算します。 |
MathArctan | 配列要素のarctan(x)関数の値を計算します。 |
MathSinPi | 配列要素のsin(pi*x) 関数の値を計算します。 |
MathCosPi | 配列要素のcos(pi*x) 関数の値を計算します。 |
MathTanPi | 配列要素のtan(pi*x) 関数の値を計算します。 |
MathAbs | 配列要素の絶対値を計算します。 |
MathCeil | 配列要素が最も近い値に切り上げられた場合の整数値を返します。 |
MathFloor | 配列要素が最も近い値に切り下げられた場合の整数値を返します。 |
MathSqrt | 配列要素の平方根を計算します。 |
MathExp | 配列要素のexp(x)関数の値を計算します。 |
MathPow | 配列要素のpow(x, power)関数の値を計算します。 |
MathLog | 配列要素のlog(x)関数の値を計算します。 |
MathLog2 | 配列要素の2を底とする対数を計算します。 |
MathLog10 | 配列要素の10を底とする対数を計算します。 |
MathDifference | 要素の差がy[i]=x[i+lag]-x[i]の配列を生成します。 |
MathSample | 配列要素からランダムサンプルを生成します。 |
MathTukeySummary | 配列要素のTukeyの五数要約を計算します。 |
MathRange | 配列要素の最小値と最大値を計算します。 |
MathMin | すべての配列要素の最小値を返します。 |
MathMax | すべての配列要素の最大値を返します。 |
MathSum | 配列要素の和を返します。 |
MathProduct | 配列要素の積を返します。 |
MathStandardDeviation | 配列要素の標準偏差を計算します。 |
MathAverageDeviation | 配列要素の平均絶対偏差を計算します。 |
MathMedian | 配列要素の中央値を計算します。 |
MathMean | 配列要素の平均値を計算します。 |
MathVariance | 配列要素の分散を計算します。 |
MathSkewness | 配列要素の歪度を計算します。 |
MathKurtosis | 配列要素の尖度を計算します。 |
MathLog1p | 配列要素の log(1+x)関数の値を計算します。 |
MathExpm1 | 配列要素のexp(x)-1関数の値を計算します。 |
MathSinh | 配列要素のsinh(x)関数の値を計算します。 |
MathCosh | 配列要素のcosh(x)関数の値を計算します。 |
MathTanh | 配列要素のtanh(x)関数の値を計算します。 |
MathArcsinh | 配列要素のarcsinh(x)関数の値を計算します。 |
MathArccosh | 配列要素のarccosh(x)関数の値を計算します。 |
MathArctanh | 配列要素のarctanh(x)関数の値を計算します。 |
MathSignif | 値を指定された仮数の桁数を持つ値に丸めます。 |
MathRank | 配列要素のランクを計算します。 |
MathCorrelationPearson | ピアソンの相関係数を計算します。 |
MathCorrelationSpearman | スピアマンの相関係数を計算します。 |
MathCorrelationKendall | ケンドールの相関係数を計算します。 |
MathQuantile | 指定された確率に対応するサンプルの分位数を計算します。 |
MathProbabilityDensityEmpirical | 乱数に対する経験的確率密度関数を計算します。 |
MathCumulativeDistributionEmpirical | 乱数に対する経験的な累積分布関数を計算します。 |
Originally posted 2019-07-30 09:53:06.